Trigonometri

Vikipedi, özgür ansiklopedi

Trigonometri, üçgenlerin açıları ile kenarları arasındaki bağıntıları konu edinen matematik dalı.

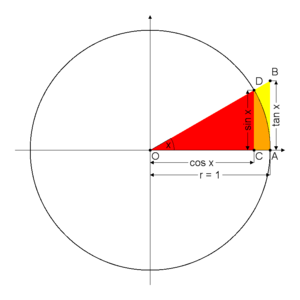
sinüs, kosinüs ve tanjant

Düzlemsel trigonometride, iki boyutlu düzlemde (ve üçü de aynı doğru üzerinde yer almayan) üç noktayı doğru parçalarıyla ikişer ikişer birleştirerek oluşturulan düzlemsel üçgenler söz konusudur. Küresel trigonometride ise, üç boyutlu kürenin iki boyutlu olan yüzeyinde (ve üçü de aynı büyük çember üzerinde yer almayan) uç noktayı büyük çember yaylarıyla ikişer ikişer birleştirerek oluşturulan küresel üçgenler söz konusudur. Küresel trigonometri Eski Yunanda astronomiye ilişkin gereksinimleri karşılamak amacıyla ortaya çıktı ve gelişti. Küresel trigonometri aslında düzlemsel trigonometriyi de tümüyle içerir, ama düzlemsel trigonometri ancak 15. yüzyıl Avrupa'sında, topografya, ticaret ve denizciliğin gereksinimleri doğrultusunda kendi başına ve küresel trigonometriden bağımsız olarak gelişmiştir. Küresel trigonometri, düzlemsel geometriden daha önce ortaya çıkıp gelişmiş olmakla birlikte, ancak düzlemsel geometrinin temel ilkelerinin bilinmesiyle daha iyi anlaşılabilir.

Düzlemsel trigonometri aslında her tür düzlemsel üçgen için geçerli olmakla birlikte, bağıntılar genellikle dik üçgenlerde tanımlanır. Açılarından biri (x) 0° ile 90° arasında olan bir dik üçgenin (düzlemsel bir üçgende iç açıların toplamı 180° olduğu için) öteki açısı 90-x'a eşittir. Böyle bir üçgende dik açının karşısındaki kenar |OD| hipotenüs, O 'nun karşısındaki kenar |CD| karşı kenar, |OC| 'ya komşu olan kenar ise komşu kenar olarak adlandırılır. Bu kenarlar birbirlerine ikişer ikişer altı farklı biçimde oranlanabilir, böylece A açısının trigonometrik fonksiyonları tanımlanmış olur.

Ğ==Açı==

Başlangıç noktaları aynı olan iki ışının birleşimine açı denir.

[OA ve [OB ışınlarına açının kenarları, O noktasına açının köşesi denir.

Konu başlıkları

[gizle]

Yönlü Yaylar [değiştir]

Çember üzerinde açı pozitif yönlü ise yay da pozitif yönlü, açı negatif ise yay da negatif yönlü olarak alınır.

Birim(Trigonometrik) Çember [değiştir]

Merkezi orijin ve yarıçarpı 1 birim olan çembere birim çember veya trigonometrik çember denir. Birim çemberin denklemi

$x^2 + y^2 =1$

şeklindedir.

Birim çemberde verilen bir $P(x,y)$ noktası;

1.bölgede ise $x > 0 , y > 0$
2.bölgede ise $x < 0 , y > 0$
3.bölgede ise $x < 0 , y < 0$
4.bölgede ise $x > 0 , y < 0$ dır.

Açı Ölçü Birimleri [değiştir]

Açıyı ölçmek demek, açının kolları arasındaki açıklığı belirlemek demektir.

Açı ölçü birimleri üç tanedir.

DERECE: Bir tam çember yayının 360 eş parçaya bölünmesiyle elde edilen her bir yayı gören merkez açının ölçüsüne 1 derece denir.

GRAD: Bir tam çember yayının 400 eşit parçaya bölünmesiyle elde edilen her bir yayı gören merkez açının ölçüsüne 1 grad denir.

RADYAN: Bir çemberde yarıçap uzunluğundaki yayı gören merkez açının ölçüsüne 1 radyan denir.Çember yayının ölçüsü 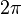$2pi$ radyandır.

Sarma Fonksiyonu [değiştir]

Reel sayılar kümesinden birim çember üzerindeki noktalara tanımlanan fonksiyona sarma fonksiyonu denir.

Sarma fonksiyonunu s ile, birim çemberi de C ile gösterirsek;

$s:R --> C$ yazilabilir.

$s(x)=P$ oldugunda $s(x+ 2k pi ) = P$ olur.

Bir Açının Esas Ölçüsü [değiştir]

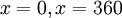a) Verilen açı $0 < x < 360$ ya da $x = 0 , x = 360$ ise;

$x$ in esas ölçüsü kendisidir.

b) Verilen açı $x > 360$ ya da $x = 360$ ise;

$x$ in 360 a bölümünden kalan esas ölçüyü verir.

c) Verilen açı $x < 0$ ise;

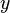$-x$ 360 a bölümünden kalan $y$ olsun.

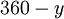O halde, $x$ in esas ölçüsü $360 - y$ dır.

Trigonometrik Fonksiyonlar [değiştir]

sinüs (kısaltılmış biçimi; sin), $sin x = frac{vert CDvert}{vert ODvert}$
kosinüs (cos), $cos x = frac{vert OCvert}{vert ODvert}$
tanjant (tan ya da tg), $tan x = frac{vert CDvert}{vert OCvert}$
sekant [sec),
kosekant (cosec) ve
kotanjant (cot)

olarak adlandırılır.

Bu tanımlardan görülebileceği gibi, bu fonksiyonlar arasında,

$tan x = frac{sin x}{cos x} , cot x = frac{1}{tan x} = frac{cos x}{sin x}$

$sec x = frac{1}{cos x} , csc x = frac{1}{sin x}$

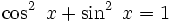${cos^2 x} + {sin^2 x} = 1$ (Pisagor teoremi)

ilişkileri vardır.

Dik Üçgenlerde Bazı Açıların Trigonometrik Oranları [değiştir]

$x$	$0=360 =2pi$	$30 =pi /6$	$45 =pi /4$	$60 =pi/3$	$90 =pi /2$	$180 =pi$	$270 =3pi /2$
$sin x$	$0$	$1 / 2$	$sqrt 2 / 2$	$sqrt 3 / 2$	$1$	$0$	$-1$
$cos x$	$1$	$sqrt 3 / 2$	$sqrt 2 / 2$	$1 / 2$	$0$	$-1$	$0$
$tan x$	$0$	$1 /sqrt 3$	$1$	$sqrt 3$	$Sonsuz$	$0$	$Sonsuz$
$cot x$	$Sonsuz$	$sqrt 3$	$1$	$1 /sqrt 3$	$0$	$Sonsuz$	$0$