Vikipedi, özgür ansiklopedi
Geometri (veya hendese), matematiğin uzamsal ilişkiler ile ilgilenen alt dalıdır. (Eski adı: Hendese. Yunanca Γεωμετρία "Geo" (yer) ve "metro" (ölçüm) kelimelerinin birleşiminden türetilmiş bir isimdir.)
Geometri, arazi ölçümü sözcüklerinden türetilmiştir. Herodot (i. Ö. 450), geometrinin başlangıç yerinin Mısır olduğunu kabul eder. Bu nedenle geometri sözcüğü Mısır kökenlidir. Kullanımı da Eflatun, Aristo ve Thales’e kadar gider. Yalnız Euclit geometri sözcüğünü kullanmamıştır. O bu sözcük yerine Elements sözcüğünü yeğlemiştir. Elements sözcüğünün Yunanca karşıtı stoicheia sözcüğüdür.
Günümüzde kullanılan doğru, yay, ışın, açı ortay, kenar ortay gibi birçok temel geometri teriminin Türkçe'leri Mustafa Kemal Atatürk'ün Geometri adlı eserinde yazılan eserde önerdiği terimlerden yararlanılarak kullanılmaya başlanmıştır.
Birkaç geometri vardır. Bizim günlük yaşamda bildiğimiz "lise geometrisi"nin adı Öklit geometrisidir. Bu geometrinin en önemli özelliği paralellik belitidir. Bu beliti sağlamayan ama geri kalan tüm belitleri sağlayan geometrilere Öklit dışı geometriler denir. Bunlara örnek olarak Hiperbolik geometri ya da küresel geometri örnek verilebilir.
İlk geometrilerin tümü, kendi doğası nedeniyle sezgiseldir. Bunlar daha çok ilk insanların çevresinde görünen doğal şekillerdir. Bu geometriler daha çok görsel türdedir. İkinci olarak şekillerin ölçülmesi aşaması gelir. Dörtgenlerin ve üçgenlerin ölçülmesi ilk kez Mısır’da Ahmes’in (İ. Ö. 1550) papirüsünde görülür.
Bu papirüs M.Ö. 1580 talihinden önce yazılmıştır, b tabanlı ve h yükseklikli ikiz kenar üçgenin alanının bh/2 olduğu verilmiştir.
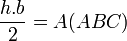
Yine aynı papirüste d çaplı bir dairenin alanının (d-d/9)2 yazımına eşdeğer olduğu yazılmıştır. Bu yazımlara göre pi sayısı yaklaşık olarak 3.1605 dolaylarındadır. Bu formül geometrik şekilden yaklaşık olarak elde edilmiştir.

Bu formül Babillilerde de aynıdır. Bu söylediğimizi kanıtlayan tabletler vardır. Çin’in yerli geometrisi de bu türdedir. İ. Ö. 1100 yıllarında yazıldığı sanılan Çinlilerin ünlü Nine Sections (Dokuz Bölüm) kitabında dik açılı üçgen ve ispatsız olarak Pisagor teoremi vardır. Daha sonraki Çin geometrilerinde ölçümleri içeren çok zeki buluşlar vardır. Yine geometrik görünümle Pisagor teoreminin ispatı yapılmıştır. Bu geometrik şekille verilen kitabın İ. Ö. 2000 yıllarında yazıldığı sanılıyor.
Hintlilerin yerli geometrilerinde de matematiksel bir ispat yoktur. Daha çok görsel ve deneysel ölçülere dayanan kuralları vardır. Bunlar da o kadar ileri bir geometri oluşturmaz. Bin yıllık bir süre boyunca kullanılan Yunan geometrisi ise daha çok görseldir. Eski Roma geometrisi daha çok kullanım alanlarına yöneliktir.
Arazi ölçümleri, şehir yerleşimleri, su kanalları ve savaş sanatında geometriyi Romalılar iyi kullanmışlardır. Fakat bunlar görsel geometriyi fazla kullanmamışlardır. Zaten görsel geometrinin kökeni Yunanistan’da başlamıştır. Bu çalışmalar ilk kez Tha-lesin (İ. Ö. 600) yapıtlarında görülür. Thales bu teoremleri Mezopotamya’da ve Mısır’da kullandıklarını görür. Altı teoremle önderlik eder ve bu teoremlerin ispatlarını yapar. Matematikte ispat yapma Thales’le başlamıştır. Thales’in bu ispatları zamanla kaybolmuş arma, ondan sonra bunları öğrenenler gelecek kuşaklara aktarmıştır. Bin yıl süren bu görsel Yunan geometrisi zamanla gerilemiş ve yeni bir çalışma getirilmemiştir.
Batı Avrupa’nın uyanmasından önceki yüzyıla kadar Yunan kültürünü ve geometrisini tam olarak müslümanlar anlamıştır. Yunan klasiklerini, geometrilerini, fen bilimlerini ve felsefelerini Arapça’ya çevirmişlerdir. Fakat ne Euclit’in ne de Apollonius’un çalışmalarına gerçek ve gözle görünür bir katkı ve ekler yapmamışlardır. Okullaşma olmadığı için gelecek gençlere bu çeviriler öğretilmemiş, bu kitaplar sadece neredeyse bir süs olarak sarayda kalmıştır. Yaptıkları hizmet, kaybolmaya yüz tutmuş Yunan klasik-ni, matematiklerini ve düşüncelerini Arapça çevirileriyle Avrupa’ya iletmişlerdir. Aslında bu da bir hizmet sayılır.

Kadın Geometri öğretiyor.Orta çağın başlangıcında Öklid unsurlarının çevirisinin canlandırılması, (yaklaşık.
1310)
Avrupa’daki karanlık çağda biri Boethius’un (510) diğeri de Euclit’in (L Ö. 300) Sements isimli kitabı vardı. Bunlardan sonra Gerbert’in (1000) ve Fibonacci’nin (1202) geometrileri sayılabilir, Ama bu geometriler İskenderiye geometrilerinden ileri bir düzeyde değildi. Avrupa’nın geometrisine yine 1482 yılında ilk baskısı yapılan Euclit geometrisi oldu. Zaten çok iyi düzenlenmiş ve yazılmış olan bu geometriler Avrupa’ya hızla yayıldı ve her tarafında bilinir oldu. Euclit’in geometrisinin ardından yavaş yavaş geometri ürünleri ortaya çıkmaya başladı, On yedinci yüzyılın başlarında analitik geometri ve 1639 yılında da Desargues’ın (1593-1662) izdüşüm geometrisi basıldı. Analitik geometri Descartes (1596 -1650) ve Fermat (1601 -1665) tarafından aynı dönemlerde yapıldı. Fermat yaptığı çalışmaları yayınlamadığı için analitik geometrinin bulunması onuru Descartes’e verildi. Analitik geometri kısaca geometri İle cebir arasındaki ilişkidir diye söyleyebiliriz. Geometri ile cebir arasındaki ilişkiyi ilk kez Descartes çıkardığı için büyük bir matematikçi olmuştur. Desargues’ın izdüşüm geometrisi matematikçilerin çok dikkatini çekmiş ve on dokuzuncu yüzyılda çıkacak olan geometricilere coşku ve esin kaynağı olmuştur.
Analitik geometri bulunduktan sonra Apollonius’un (İ. Ö. 262-190) konikleri sentetik ve analitik olarak yeniden incelenmiştir. Sadece konikler değil, eski Yunan geometrisi yeniden analitik olarak gözden geçirilmiştir. Sentetik geometrinin tüm problemleri bir kezde analitik olarak kanıtlanmıştır.
Öklid Geometrisi [değiştir]
Euclit geometrisinin temeli nokta iie başlar. Pisagorcular noktayı küçük bir zerre olarak tanımlamışlardır. Bu tanım aslında Aristo’dan (İ. Ö. 340) alınmıştır. Eflatun (i. ö. 380), noktayı bir doğrunun başlangıcı olarak tanımlamıştır. Bu kez doğru nedir sorusu karşımıza çıkmaktadır. Altıncı yüzyılda yaşayan Simplicus, uzunluğun başlangıcı ve buradan doğru uzar. Ayrıca bölünemez diye noktayı tanımlamıştır. Hiçbir parçası olmayan ize nokta denir tanımını Euclit (İ.Ö. 300) yapmıştır. Heron (50) da aynı sözcüğü kullanmış, noktayı boyutsuz bir limit veya doğrunun bir limitidir şeklinde söylemiştir. Capella (460), hiçbir parçası olmayan şeye nokta denir demiştir. Modern yazarlar noktayı sanki tanımlı bir limit kavramıdır diye almışlardır. Dönemimizde de, nokta kabul edilen bir kavramdır. Noktayı kabul ettikten sonra işler kolaylaşır.
Eflatuncular, ensiz uzunluğa doğru demişlerdir. Aynı tanımı Euclit de almıştır. Yani noktanın hareketinden doğru elde edilir. Doğrunun hareketiyle yüzey ve yüzeyin hareket ile de hacim oluşturulur. Bundan sonra doğru, yarı doğru, doğru parçası, yüzey, düzlemsel yüzey, açı, çember, daire, çap, yarıçap, paralel doğrular ve dik doğrular gibi bir dizi geometrik tanımlar getirilmiştir.
İspatlanamayan gerçeklere aksiyom ismi verilir. Açıkça görülen fakat ispatlana-mayan gerçeklere de postülat denir. Euciit’in geometrisi tanım, aksiyom ve postülatlar üzerine kurulmuştur. Zaten matematik aksiyomatik bir düşüncedir. Belli şeyleri kabul ederseniz: onun üzerine matematiği kurarsınız.
Öklid'in aksiyomları [değiştir]
Şimdi, Euclit’in beş aksiyomunu yazalım; 1. Aynı şeye eşit olan şeyler eşittir,2. Eşit şeylere eşit çokluklar eklenirse sonuç yine eşittir,3. Eşit şeylerden eşit çokluklar çıkarılırsa sonuç yine eşittir,4. Birbirleriyle çakışan şeyler birbirine eşittir,5. Bütün, parçalarından büyüktür.
Şimdi de postülatlara bazı örnekler verelim.
1. iki noktadan bir doğru geçer,
2. iki nokta arasındaki sürekli doğru sonludur,
3. Bir noktadan eşit uzaklıktaki noktaların geometrik yeri bir çemberdir,
4. Tüm dik açılar birbirine eşittir,
5. İki doğru bir doğru ile kesildiğinde kesenin bir tarafında oluşan iki iç açının toplamı 180 dereceden küçükse, bu iki doğru bu 180 dereceden küçük açıların bulunduğu tarafta kesişirler.
Bu postülatlar daha sonraki Yunanlı bilginler tarafından çok İncelendi ve geliştirildi. Sidonlu Zeno (İ. Ö. I. yüzyıl) farklı iki doğrunun ortak bir doğru parçası yoktur. Dördüncü ve beşinci postulatların birer teorem olduğu yine ileri sürülmüştür. Proclus (460) dördüncü postulatı bir teorem olarak almış, ispatlamaya çalışmış fakat başaramamıştır. Bu postülatın tersinin doğru olmasının gerekmediğini de ileri sürmüş ve bunu ispatlamıştır. Saccheri (1773) bu postülatı farklı bir yolla ispatlamıştır.
Beşinci postülat [değiştir]
Matematikte en çok tartışılan ve önemli olan beşinci postülattır. Bu postülat daha çok paralellik postülatı olarak bilinir. Yani, bir doğruya dışındaki bir noktadan bu doğruya yalnız bir tek paralel çizilir ifadesi beşinci postülata eşdeğerdir. Bu nedenle beşinci postülat daha çok bu ifadeyle tanınır. Tarih boyunca bu postülatı ispatlamak için girişimlerde bulunulmuştur. Bunlardan önemli girişimler Ptolemy (85 - 165), Nasirettin elTusi (1200), VVallis (1660), Saccheri (1733), Lambert (1766), Legendre (1794) ve diğerleri tarafından yapılmıştır.
Playfair postülatı [değiştir]
Proclus’un postulatına bir alternatif Playfair (1795) getirilmiştir. Playfair’in dünyaya tanıttığı postulat da şöyledir. Bir doğruya dışındaki bir noktadan yalnız bir tek paralel çizilir. Ya da kesişen iki doğru bir doğruya ve aynı doğruya paralel olamazlar. Aslında Playfair’in postulatı pratik olarak 1795 tarihinden önce biliniyordu. Çünkü, bu postülatı Joseph Fenn, Euclit’in Elemenfs isimli kitabını 1769 yılında Dublin’de yayınladığında »azmıştı. O da, iki paralel doğrudan birini kesen doğru diğerini de keser şeklindeydi. Proclus (460) tarafından verilen bu postülat VVilliam Ludlam (1785) tarafından da yazılmıştı. Zaten bu ileri sürülen postülatların tümü Euclit’in Elements isimli kitabının birinci cildinin otuz birinci sayfasında vardı. Yukarıdaki yazarların sunduğu postülatlar Euclit’in beşinci postulatının eşdeğer söylenişleriydi.
İlkel geometrinin düzlemsel geometri problemlerinin temelleri Euclit’in Elements isimli kitabında vardı. İkiz kenar bir üçgenin taban açıları da birbirlerine eşittir. Euclit’in birinci kitabının beşini önermesi olarak geçen bu teorem, ilk kez Thales (İ. Ö. 600) tarafından ispatlandığını Proclus (460) söylemektedir. Yine aynı teoremin farklı bir yoldan Pappus (300) tarafından ispatlandığını Proclus söylemektedir. Bu teorem Ortaçağ boyunca matematikçilerin dikkatini çekmiş. Roger Bacon (1250) da bu teoreme değinmiştir.
Thales’in benzerlikleri [değiştir]
Benzer üçgenler kavramı Thales (M.Ö. 600) ve onun öncesinden başlamış, Eude-mus’la (M.Ö. 335) devam etmiştir. Benzer üçgenler Thales tarafından yanına varılamayan uzaklıkların ölçülmesinde kullanılmıştır. Bugün orta dereceli okullarda okutulan Thales teoremleri çok sevilen kurallardır. Yalnız, yanına varılamayan uzaklıkları ölçen ilkel bazı araçlar Babilliler tarafından yapılmıştır. Euclit, Babillilerin bu aletinin karışık bir şekil olduğunu yazar. Bir şekle uydurup ispatını da veremez. Bu şeklin ispatını daha sonraki yüzyıllarda el Nairizi yazarı bilinmeyen birinin açıklamalarına dayandırarak verir Bunun en iyi ürünlerini de Napolyon’un (1769 -1821) matematikçileri almıştır.
Thales’in benzerliklerini en iyi ve pratik olarak uygulamalarını Rönesans yazarları kullanır. Bunların en güzel şekillerini Belli’nin (1570), 1569 yılında yayınladığı çalışmasında görebiliriz.
Sevdiklerimize onları sonsuza kadar seveceğimizi söyleriz, hatta buna biz de inanırız. Oysa sonsuz o kadar uzak ki..- Sonsuzda ne biz varız, ne Dünya var, ne Güneş var, ne de Samanyolu var. Tüm kumsallardaki tüm kum tanelerini sayabiliriz. Ya da evrenin bilinen ölçüleri içinde kaç tane molekül olduğunu bile hesaplayabiliriz. Bu değerlerle düşünmeye başladığımız zaman içinde yaşadığımız zaman diliminin kıymetini daha iyi anlamaya başlarız. Onun ne kadar kısa, ne kadar değerli olduğunu görürüz. Matematikçilerin hayatı seven ama ciddiye almayan yaklaşımlarında bu sonsuz kavramıyla haşır neşir olmalarının bir etkisi var mıdır dersiniz?
Peki, bu sayma işlemlerinde kullandığımız sayıların kendilerini saymaya kalkarsak? Kaç tane tam sayı vardır dersiniz.? Elbette sonsuz tane. Bu sonsuz kavramını kullanarak ondan daha büyük sonsuz kavramları da düşünebiliriz, Örneğin: bir doğru üzerindeki herhangi iki farklı nokta arasındaki nokta sayısı daha büyük bir sonsuz değere karşılık gelir. İnsanoğlu sonsuz kavramına ancak kendini tekrar eden ve döngüye giren durumlarla yaklaşabiliyor. Sonsuz denince akla bu kavramı sanatta en iyi biçimde yakalayan ünlü grafik sanatçısı Esher geliyor. Birbirini çizen eller, birbirine dönüşen varlıklar ve içine girdiğiniz zaman sonsuza kadar çıkamayacağınız resimler.
Geometri sözcüğü Dünya’nın ölçümü anlamına gelir. Bu bilim dalı başlangıçta düzlemdeki ve uzaydaki şekillerin incelenmesini konu edindi. Adı geçen şekiller somut nesnelerden türemelerine karşın, geometri deneysel yöntemlerin kullanımını çok erken bıraktı. İspat öne çıktı. Bunun tersine, şekilleri gerçek nesnelerin ideal biçimine indirgemeye çalıştı. Parçaları olmayan nokta, bütün noktalarda kendine benzeyen doğru ve yüzeyler birer aksiyom olarak alındı. Öte yandan geometri, gözlemi de ölçmeyi de kullanmayan postülatlar ve sonuçlarla işleyen bir kanıtlama biçimine başvurdu. Babilliler ve Mısırlılarda önceleri ispat yoktu ve daha çok deneme yöntemi kullanılıyordu. Ama Thales (İ. Ö. 626 - 545) ve Euclides’le (İ. Ö. 300) gelen geometri tümüyle ispatlıydı.
Descartes ve düzlem geometrisi [değiştir]
Cebirsel yöntemlerin etkinliğini ve gücünü gösteren Descartes (1596 -1650), her tür düzlem geometri problemini bir denklemler dizisine indirgedi. Yani geometriyi aritmetikleştirdi. Bu dönemden sonra, sayısal koordinatlara dayanan bir gösterim biçimi kullanıldı ve şekilleri fonksiyonlar olarak ele aldı. Analitik geometri adı verilen bu yöntem, büyük bir ilerleme kaydetti. On sekizinci yüzyılda üç boyutlu uzay ve yüzeyler kuramını da kapsamına aldı. Bununla birlikte bu yaklaşım, yanlış olarak birleşmiş geometri de denilen arı geometrideki şekillerin sezgisel anlamından uzaklaştı.
On dokuzuncu yüzyıl boyunca, Rönesans’tan beri sanatçılar tarafından araştırılan gösterim tekniklerine, izdüşümsel geometri sistemleştirilerek matematiksel bir içerik kazandırdı. Böylece, bireşimsel yaklaşımın geri dönüşüne tanık olundu. Çünkü, Fransız matematikçi Poncelet (1788 -1867) ve Chasles (1793 -1880), şekilleri, bazı özelliklerini koruyarak değiştiren dönüşümlerin önemini gösterdiler.
Klasik geometri sadece pergel ve cetvel yapımı üzerinedir. Ancak daha sonraları bu yapımın soyut cebirle olan bağlantısı anlaşılınca geometri ile cebir arasında sınırlar kaybolmaya başlamıştır. Geometrideki kilometre taşları şöyle sıralanabilir. İsa’dan önce Thales, Euclides. Apollonios, Archimedes ilk akla gelenlerdendir. Daha sonra Descartes (1637), Desar-ques (1639), Lazer Carnot (1803), Jean Victor Poncelet (1822), Janos Bolyai (1823), Mİchei Chasles (1837), N. Lobaçevsky (1840), Bernard Riemann (1867), C. Fe1ix Klein (1872), David Hilbert (1899) ve Albert Einstein (1921) olarak sayılabilir
Geometri'nin Kullanım Alanları [değiştir]
Geometri günlük yaşamın hemen her alanında gereklidir. Geometride uzunluk, alan, yüzey, açı gibi kavramlar bazı nicelikleri belirlemede kullanılır. Geometri’nin en çok iç içe olduğu dallar cebir ve trigonometri, mimarlık, mühendislikler (Yol, köprü, yapı, makine, gemi ve uçak yapımı; maden, su ve elektrik işleri gibi bayındırlık ve zanaatla ilgili teknik çalışmalar, vb.) , endüstiryel alanlar, simülasyonlar, bilgisayar programları ve grafikleri, sibertenik, tasarım, sanat vb.dir Geometrinin kullanılmadığı meslek ya da alan yok gibidir desek yerinde olur.
Geometri ve Sanat [değiştir]
Geometri ve sanat birbirleri ile bağlantılı olup birbirlerini destekleyen iki bilimdir. Sanatta geometrinin kullanımı yüzyıllardan beri süregelmiştir.Özellikle mimari yapılarda geometriden faydalanılmıştır. En bilindik olarak da Mimar Sinan eserlerinde geometriden oldukça yararlanmış ve muhteşem eserler vermiştir. Eserlerinde geometriyi çok iyi kullanmış olması eserlerinin sağlam yapılar olmasına büyük bir katkı sağlamıstır.
Sanat eserlerinin geometrik olması onlara estetik değerler kazandırmıştır. Ünlü ressam Leonardo da Vinci’nin resimde vücut oranları üzerine yaptığı çalışmalar, çizdiği eskizler bulunmaktadır.Bu orana Altın Oran denmektedir.
Geometri ve Tasarım [değiştir]
Gazete, dergi ve amblem tasarımları günümüzde profesyonel kadrolar tarafından gerçekleştirilen önemli bir iştir. Basın-yayın organları ve firmalar bu gerçeğin bilincinde olduklarından kalabalık kadroları bu işte görevlendirmişlerdir.
Tasarım başlı başına bir sanat sayılır. Tasarımcılıkta geometri kısmen işe yarar. Daha çok oran ve paraleliklerin önem kazandığı logo ve amblem tasarımında kullanılır.
Tabiattaki geometrik şekilleri fark eden insanlar geometriyi hayatlarında uygulamışlardır.Zamanla logo ve amblemler ortaya çıkınca insanlar logo ve amblemlere de geometrik anlamlar yüklemişlerdir. Bunun sonucunda da umursamadığımız en basit bir amblem dahi geometrik bir eser haline gelmiştir. Örneğin; her gün yollarda rahatlıkla görebileceğimiz, Mercedes, Mitsubishi ve Renault gibi ünlü araba markalarının ablemleri; iyinin içindeki kötü, kötünün içindeki iyi sembolü olarak bilinen Yin-Yang sembolü ve bugün İsrail Devleti'nin kullandığı asıl ismi Davut Yıldızı olan bayrak geometrik birer eser sayılabilir.
Geometri ve Perspektif [değiştir]
Resimlerde uygulanan perspektif izdüşümsel geometrinin somut uygulamalarından biridir.
Perspektif üzerine ilk kitabı 1453’te Leon Battista Alberti kaleme aldı; Açık pencere gibi duran bir dikdörtgen çiziyorum ve buradan resmedilecek nesneye bakıyorum
Burada tek bir gözün gördüğünü tabloya yansıtmak, daha matematiksel bir anlatımla, tablo düzleminde, kişinin bir gözünün merkez alan bir izdüşümle görüntüyü oluşturmak söz konusuydu. Uzaklıkları ve açıları büyük değişimlere uğratan bu gösterim biçiminden kaynaklanmış teknik problemleri çözmek için birçok kitap yazıldı, birçok alet geliştirildi. 17.yy’da Desargues, perspektif tekniğini matematiksel olarak açıklayan ilk kişi oldu.
Geometri ve Simülasyon [değiştir]
Çağımızda yaygın olarak kullanılan simulasyon teknolojisi, gerçek olmayan bir nesnenin, durumun veya resmin; gelişmiş bilgisayar teknikleriyle taklit edilerek gerçeğine benzetilmesidir.
Üretilecek olan ürünün önceden bilgisayar ortamında modellenmesi konusunda büyük bir gelişme ortaya koyan bu teknolojinin birçok sanayi dalında sıklıkla kullanılmaktadır.
Geometri ve Haritacılık [değiştir]
Yer epilsoidini harita düzlemi üzerinde matematiksel olarak gösterme yöntemine “Harita İzdüşümü” denir. Bu yöntem; uygun izdüşümler, eşdeğer izdüşümler ve perspektif izdüşümler gibi sistemleri kapsar. Genellikle izdüşüm sistemi harita çizecek olan kişinin amacına göre seçilir. Haritacalık alanında genel olarak Küresel Geometri kullanılmaktadır.
Geometri ve Mimari [değiştir]
Çağdaş mimarîde düzenli yüzeyler, özellikle betonun kullanımı sonucunda büyük bir başarı kazandı. Çünkü bu yüzeylerin doğrularla oluşturulması beton kalıplarının yapımını kolaylaştırmaktaydı.
Tokyo Olimpiyat Stadyumu'nda "Hiperbolik Parabolit" ; Münih’deki Olimpiyat Stadyumu'nda ise "Eliptik Parabolit" ve "Tek Yaygılı Hiperbolit" mimari şekiller kullanılmıştır.
Fransa’daki Chartres Katedrali dönemin “gizli geometri” (secret geometry) ya da “kutsal geometri” (sacred geometry) olarak adlandırılan ilkelerine göre yapılmıştır.